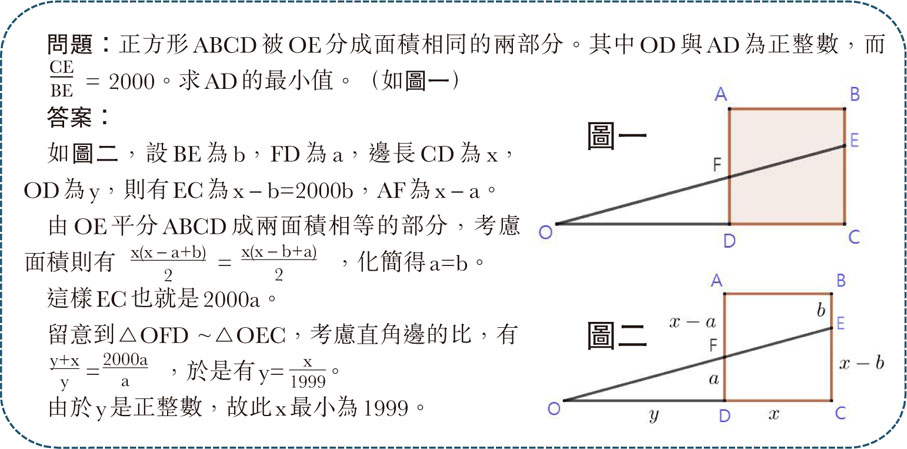
題解裏先用代數表示幾條邊，發現a和b相等，之後用了相似三角形的性質，對應邊比例相同，化簡後用整數的性質，於是找到了邊長的最小值。

設未知數的做法有很多方式，除了題目關鍵資料中，數值為整數的邊設成x與y以外，設為a和b的邊要是用其他方式去表達也可能更複雜。若想用少一些代數符號去表示的話，b可以寫成x/2001，對於平常的解難思路來說，這樣去表示各邊普遍會較方便計算，只是對於這題來說，反而會麻煩。

其中，發現a和b相等的一步用到了代數化簡。其實若發揮點想像力，想像正方形被一條直線分成兩個面積相等的部分，好像正方形三文治被切了一刀那樣，就很容易明白a和b兩邊一樣，這是通過日常生活經驗可以知道的，題解只是用數學式表達得仔細些。先有直觀的結論，再用數學上嚴謹的論證，也是探索題目的好方法。

另外，這題用坐標幾何來計算也是一個好的思考方向。比如用O作原點，OD為x軸，可以考慮OE的直線方程，再用邊長表示各點坐標。不過，用坐標幾何時未知數就要避免用x和y，以免跟方程裏的x和y混淆，值得讀者嘗試一下。

題解最後一步用到整數的性質，解得邊長的最小值，這一步事前未必能預料得到，從題目來看，限制邊長大小的條件並不明顯，比如沒有明顯的不等式之類會限制邊長，從而找到最小值。在探索後才發現，關鍵的限制是不太惹人注意的整數條件，所以完成後有些驚喜感以及探索的趣味。

這題在競賽入門階段也算是中等難度，需要學生做較長篇幅的推論，設未知數上要有巧思，推論上又需穩妥。此外還要有意識去找尋邊長與OD的關係，嘗試找尋兩條整數邊的關係，又要找到限制條件。競賽入門階段，學生初接觸競賽數學時在解難上要有方向感，也不是容易的事情。

題目有引入直觀想像的部分、較長篇幅的推論部分，有一題多解的可能，最後整數條件限制了關鍵數值，突破許多課內數學的經驗，令學生開闊眼界。● 張志基0

香港數學奧林匹克學校

簡介：奧校於1995年成立，為香港首間提供奧數培訓之註冊慈善機構(編號：91/4924)，每年均舉辦「香港小學數學奧林匹克比賽」，旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊，獲免費培訓並參加海內外重要大賽。詳情可瀏覽：www.hkmos.org。