這次談一道關於正多邊形的題目。

問 題：正2n邊形外接半徑為5的圓，由圓上任意一點，與該多邊形各頂點距離的平方，加起來是600。求n。

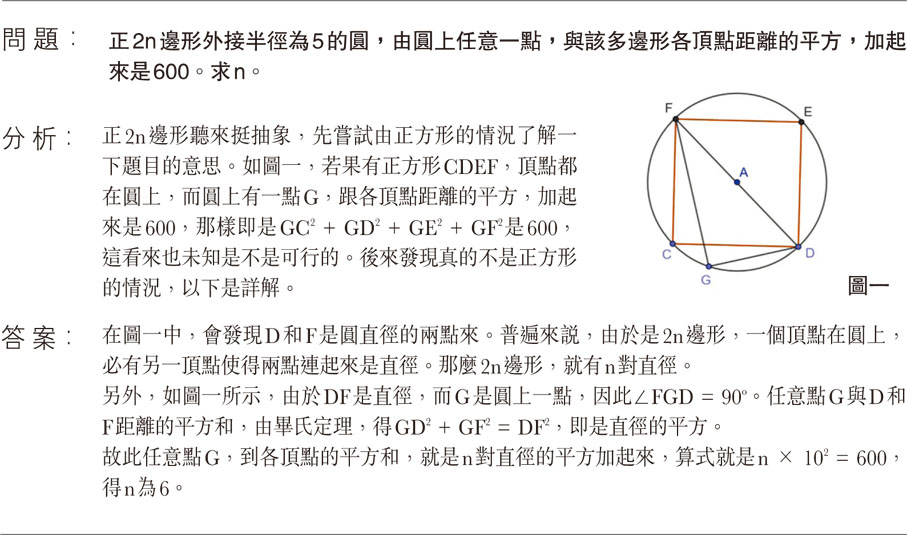
分 析：正2n邊形聽來挺抽象，先嘗試由正方形的情況了解一下題目的意思。如圖一，若果有正方形CDEF，頂點都在圓上，而圓上有一點G，跟各頂點距離的平方，加起來是600，那樣即是GC2 + GD2 + GE2 + GF2是600，這看來也未知是不是可行的。後來發現真的不是正方形的情況，以下是詳解。

答 案：在圖一中，會發現D和F是圓直徑的兩點來。普遍來說，由於是2n邊形，一個頂點在圓上，必有另一頂點使得兩點連起來是直徑。那麼2n邊形，就有n對直徑。

另外，如圖一所示，由於DF是直徑，而G是圓上一點，因此∠FGD = 90o。任意點G與D和F距離的平方和，由畢氏定理，得GD2 + GF2 = DF2，即是直徑的平方。

故此任意點G，到各頂點的平方和，就是n對直徑的平方加起來，算式就是n × 102 = 600，得n為6。

問題中的難點，在於一開始未用具體的多邊形來看時，未必想像到圓上任意點會連到直徑上的兩點，而且合起來時剛好是直角三角形。正多邊形、外接圓形的情況下，有許多對直徑不是必然的，要邊數剛好是雙數才行。題目當中，任意點到頂點的距離取平方，看來繞的彎挺多的，未想通前，好像條件都很任意，於是令人覺得複雜。

這題在奧數來說，算是入門到中階左右，有時一兩個巧妙的彎，令人一時間想不通，可能那點陌生感，就足夠令人卻步了，不一定是長篇的推論才會把人嚇怕。年輕時志向遠大一點是好事，至少能令自己涉獵各樣的知識，充實思想，在鍛煉中能了解自己強項和弱點。

只是志向遠大得來，也要量力而為，看清楚什麼層次的題目是自己有足夠的興趣和動力去挑戰。要是很早就去挑戰一些一小時多一題的題目，對自己來說可能太辛苦。現在網上資源多，也有網上書店，比較容易找到不同層次的競賽題目。

學數學的過程中，能找到自己有興趣做下去的題目，自得其樂，是好事來的。最怕是學到相當水平之後，表面有點成績，但日子苦得想放下來，那就挺可惜。

長遠來說，有些人的生活裏會需要多點數學，要懂一些難的，也有些人沒那麼大的需要，只需要懂一些淺的。學過奧數，見識過數學的另一些面貌，能夠延續這點興趣，令生活裏多一點健康的樂趣，對人生也有益處。

奧數作為一種生活的樂趣，有個好處，就是需要的數學知識基礎比較少。若是一些大學的數學書，一下子要掌握一套理論，功夫就多了，生活忙碌時，未必有這點精神和時間。●張志基

簡介：奧校於1995年成立，為香港首間提供奧數培訓之註冊慈善機構(編號：91/4924)，每年均舉辦「香港小學數學奧林匹克比賽」，旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊，獲免費培訓並參加海內外重要大賽。詳情可瀏覽：www.hkmos.

●香港數學奧林匹克學校 org。