這次談談一道四位數的問題。
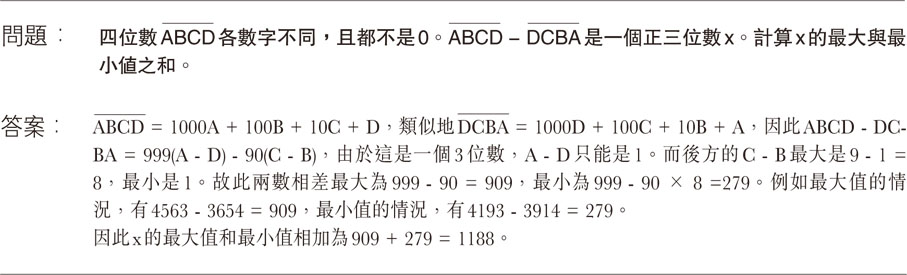
問題:四位數ABCD各數字不同,且都不是0。ABCD - DCBA是一個正三位數x。計算x的最大與最小值之和。
答案:ABCD = 1000A + 100B + 10C + D,類似地DCBA = 1000D + 100C + 10B + A,因此ABCD - DCBA = 999(A - D) - 90(C - B),由於這是一個3位數,A - D只能是1。而後方的C - B最大是9 - 1 = 8,最小是1。故此兩數相差最大為999 - 90 = 909,最小為999 - 90 × 8 =279。例如最大值的情況,有4563 - 3654 = 909,最小值的情況,有4193 - 3914 = 279。
因此x的最大值和最小值相加為909 + 279 = 1188。
解題中先把四位數變成代數式,然後找相差時,把類似的項放在一起考慮,最後估算出最大最小值的大小。
這當中有些細節要注意,比如A - D只是1,原因是若果大一點時,乘上999之後,就接近2000了,那之後的90即使乘以9,也會出了個四位數來。後面也有個細節,比如C - B為什麼最小是1,從表面來看,最小好像可以是負數,但那樣前方的999加上個正整數,又會是四位數。這些想一想其實也容易明白,只是補充一下,看來就淺白些。
話說回來,其實把相差的算式,寫成999(A - D) - 90(C - B)這個樣子,也需要有足夠經驗。始終兩數相減起來,直接的形式,還不過是一道有四個未知數的算式而已,即使看來系數有部分相同,但寫出來後,能找到許多有用的線索,或者聯想起可以做估算,不是那麼直接就可以想得到的。
後來估計到了最大最小值,那是不是就可以直接相加出答案了呢?這道題目好像可以,只是謹慎一點,還是先找個具體例子,說明這樣的情況真個可能,有相關的數字,會找到最大,又有另一組數字,會找到最小,那才好說這些最大最小值是真的可以達到。這樣就避免了運算一大堆之後,以為估計到了最大最小值,後來才知道,還有其他隱藏條件令到這些數值不會出現。
這些關於數字的問題,各個數字用上了代數,然後套入條件後,多數都是一些不定方程之類,未知數挺多,要在觀察算式之中看到一些特徵,然後思路才容易開展。
看答案時,一直看着別人的思路,好像有人帶着自己走路,那當然容易一點;若是自己走,就是要找到個好看的代數形式,恐怕也有點難。
上方的題目,從難度來說,若是放在高小的程度,就算是偏難的,到了中學時,用來入門也就挺好,要是學生到了高中才學奧數,之前未接觸過的,做起來也不算易。
其實奧數除了在學生時代用來鞏固基礎和提升能力以外,一些數學愛好者在工作之後,也會用來消閒一下。這時候,奧數題的角色,就有點像流行曲和書畫,是一些技藝,有消遣作用。有時年長了,對數學仍有一點興趣,跟身邊的青少年也可以談一點數學,那樣社會的數學文化豐厚了,好的想法也容易有了土壤,容易生根發芽,是好事來。
◆ 張志基
簡介:奧校於1995年成立,為香港首間提供奧數培訓之註冊慈善機構(編號:91/4924),每年均舉辦「香港小學數學奧林匹克比賽」,旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊,獲免費培訓並參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
◆香港數學奧林匹克學校

評論