【奧數揭秘】三粒骰子
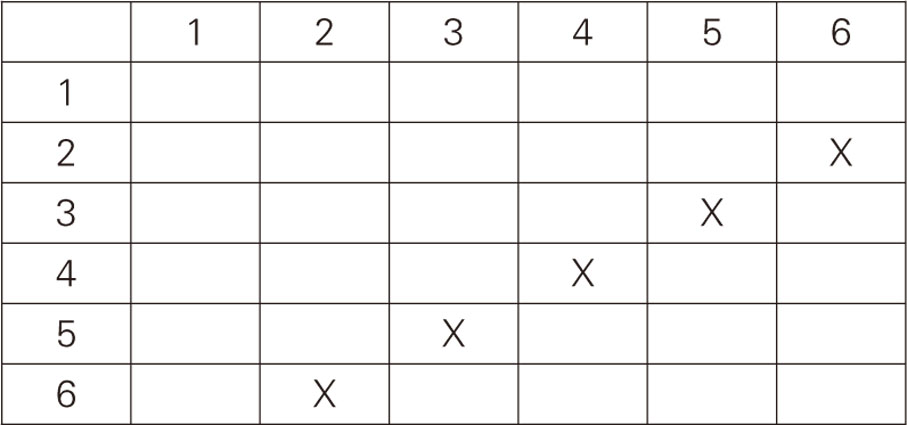

平常談起擲骰子的情況,大都是問與概率相關的問題,最簡單的就是點數為1至6的骰子裏,擲到1的機率是[1][6] 。若果講到兩粒骰子的情況,比如要點數加起來是8,那樣數起來,就有(2,6)、(3,5)、(4,4)、(5,3)、(6,2),共5種情況,機率為[5][36] 。注意這裏(2,6)和(6,2)要分兩種情況來計算,直觀上也是合理的,因為擲出2和6的情況,大概比擲出4和4是更多。處理這些擲兩粒骰子後加起來多少點數,概率又是多少的問題,畫個表是個好方法,比如剛才討論的情況,可以畫到這樣,然後就知道多少情況加起來是8,又知道總共有多少情況。
要是擲三粒骰子,那又怎樣呢?畫表的方法只在兩粒骰子時才用得到,加到三粒骰子,就很難畫成立體圖表。平常做這些問題時,要清楚有多少個情況,常用的想法都可以用樹形圖,然後先列舉,再找規律,引入加法和乘法,那就容易數一些。這次介紹一個比較特別、用上了多項式乘法的想法。
問 題:擲三粒骰子,然後把點數加起來時,總和是14的情況有多少個?
答 案:考慮(x + x2 + x3 + x4 + x5 + x6)3的展開式,然後x14找的系數,就是答案。把算式的3次,分成1次和2次相乘,則可化成(x + x2 + x3 + x4 + x5 + x6)(x2 + 2x3 + 3x4 + 4x5 + 5x6 + 6x7 + 5x8 + 4x9 + 3x10 + 2x11 + x12)
右方括號裏的算式好像很長,其實系數依次就是12345654321 = 1111112。至於為什麽是這樣的順序,讀者也可以自己思考一下。展開後,x14的系數,就是那些2次與12次的系數相乘,3次與11次的系數相乘,諸如此類,然後相加,具體而言,就是1 + 2 + 3 + 4 + 5 = 15。
也就是說,三粒骰子,點數加起來是14的情況,有15個。
題解裏的方法,在三粒骰子的情況下,與用列舉的方法相比,未必特別快。只是若推論得遠一點,想想四粒骰子的點數加起來是20之類的,由於那些系數挺有規律,計算起來就有優勢。
另外,這次問三粒骰子的情況,只是情景比較具體的問題,若果數學化一點來表達,就會變成a + b + c = n,其中n是給定的正整數,而a、b和c是一定範圍內的正整數時,有多少組解的問題,這算式也算挺常見的。這裏也見到數理之間錯綜複雜的應用,就是幾個數加起來是一個固定的數,找多少個解,也可以用多項式的系數來思考,這個憑直觀大概都是想像不到的。
這次談用多項式系數來計數的方法,說到底也只是其中一個方法,用起來效果好壞,就要看實際情況,再作出適切選擇。事實上,不管是這裏寫的心得,還是日常看文章見到的各樣生活經驗,應用前都要理解得通透,然後靈活適切地應用,才有好效果,絕不可把想法生搬硬套。 ◆ 張志基
簡介:奧校於1995年成立,為香港首間提供奧數培訓之註冊慈善機構(編號:91/4924),每年均舉辦「香港小學數學奧林匹克比賽」,旨在發掘在數學方面有潛質的學生。學員有機會選拔成為香港代表隊,獲免費培訓並參加海內外重要大賽。詳情可瀏覽:www.hkmos.org。
◆香港數學奧林匹克學校
